应用XCT断层扫描技术和GAN深度学习模型的多孔介质微观结构定量研究

doi:10.16258/j.cnki.1674-5906.2024.01.013

生态环境学报 ›› 2024, Vol. 33 ›› Issue (1): 119-130.DOI: 10.16258/j.cnki.1674-5906.2024.01.013

应用XCT断层扫描技术和GAN深度学习模型的多孔介质微观结构定量研究

李雪莹¹^,²^,³(), 陆峥²^,³, 何源¹^,²^,³, 杨晓帆²^,³^,^*()

1.北京师范大学/环境演变与自然灾害教育部重点实验室，北京 100875
2.北京师范大学/地表过程与资源生态国家重点实验室，北京 100875
3.北京师范大学地理科学学部，北京 100875

收稿日期:2023-08-04 出版日期:2024-01-18 发布日期:2024-03-19
通讯作者: *杨晓帆。E-mail: xfyang@bnu.edu.cn
作者简介:李雪莹（1999年生），女，博士研究生，主要从事地下水溶质运移模型研究。E-mail: lixueying@mail.bnu.edu.cn
基金资助:
北京师范大学地表过程与资源生态国家重点实验室自主研究自由探索项目(12807-370100018);北京师范大学环境演变与自然灾害教育部重点实验室2023年度研究生开放课题(120230629)

Reconstruction of Porous Media Microstructure Via X-ray Computed Tomography and Generative Adversarial Networks

LI Xueying¹^,²^,³(), LU Zheng²^,³, HE Yuan¹^,²^,³, YANG Xiaofan²^,³^,^*()

1. Key Laboratory of Environmental Change and Natural Disaster, MOE/Beijing Normal University, Beijing 100875, P. R. China
2. State Key Laboratory of Earth Surface Processes and Resource Ecology/Beijing Normal University, Beijing 100875, P. R. China
3. Faculty of Geographical Science, Beijing Normal University, Beijing 100875, P. R. China

Received:2023-08-04 Online:2024-01-18 Published:2024-03-19

摘要/Abstract

摘要：

物质在土壤中的迁移转化行为是研究地下水动力学的核心问题。定量化表征多孔介质拓扑结构并计算分析相关表面形态学参数，为研究复杂介质内物质运移微观机理提供了重要的数据基础和参数。应用微米级X射线计算机断层扫描(XCT)和图像处理技术，结合前沿的机器学习算法重建和定量分析多孔介质微观结构，可快速、批量创建高分辨率的复杂多孔介质研究样本。首先采用XCT技术，提取石英砂和散装土壤两类典型多孔介质的微观孔隙结构；而后基于生成对抗神经网络(GAN)模型重构复杂多孔介质的微观空间结构，与XCT扫描图像进行交叉验证；最后，计算获取Minkowski形态学参数，并基于多孔介质微观结构开展计算流体力学（CFD）数值模拟，计算石英砂和土壤多孔介质内的流动特征和渗透率。结果表明：1）GAN生成的合成数据与原始数据符合KS同分布，说明GAN能够成功合成与原始图像结构空间分布模式一致的图像；2）Minkowski宏观参数评价误差的较小，KS同分布结果表明，多孔介质样本的结构异质性会在一定程度上影响GAN模型的计算精度和效率；3）OpenFOAM模拟计算得到的渗透率结果表明，GAN模型生成的多孔介质图像与原始图像具有一致的统计特征和物理性质。综上，综合运用前沿的XCT扫描、图像处理技术和机器学习算法，构建了土壤微观结构重建和定量分析模型，并结合多孔介质形态学和计算流体力学方法对模型进行了验证和分析。该研究为多孔介质微观结构研究提供了新技术和新方法，为进一步研究复杂多孔介质内溶质运移提供了科技支撑。

关键词: 多孔介质, XCT断层扫描, GAN模型, Minkowski参数, 计算流体力学, 渗透率

Abstract:

Quantitatively analyzing the microstructure of porous media and calculating the morphological parameters provide an important data basis for studying the mechanism of solute transport in complex media. Micro X-ray computed tomography (μ-XCT), image processing technology, and cutting-edge machine learning algorithms were applied to efficiently reconstruct high-resolved microstructures of porous media, so that the relationship between microscopic pore structure and macroscopic solute transport mechanisms could be revealed. First, XCT combined with image processing method was used to capture the pore structure of quartz sand and bulk soil; then, the Generative Adversarial Network (GAN) reconstructed the complex porous media and was cross-validated via the XCT images; finally, the Minkowski parameters were calculated from the original data and the synthetic data via ImageJ software, and a computational fluid dynamics (CFD) simulation was applied to simulate the permeability of quartz sand and soil samples. Results demonstrated that the images generated by the GAN model were statistically consistent with the original images; as the heterogeneity effect of the porous media increase, the accuracy and efficiency of GAN model would decrease to some extent. This study presented new methods for studying the morphology of porous media, as well as providing scientific and technological support for the relationship between the microstructure and solute transport behavior of complex porous media.

Key words: porous media, X-ray computer tomography (XCT), generative adversarial networks (GAN), Minkowski functionals, computational fluid dynamics (CFD), permeability

中图分类号:

X144

李雪莹, 陆峥, 何源, 杨晓帆. 应用XCT断层扫描技术和GAN深度学习模型的多孔介质微观结构定量研究[J]. 生态环境学报, 2024, 33(1): 119-130.

LI Xueying, LU Zheng, HE Yuan, YANG Xiaofan. Reconstruction of Porous Media Microstructure Via X-ray Computed Tomography and Generative Adversarial Networks[J]. Ecology and Environment, 2024, 33(1): 119-130.

图/表 16

图1 多孔介质柱实验与三维XCT重建数据集

Figure 1 XCT reconstruction dataset of porous media column

表1 XCT扫描参数

Table 1 Parameters of XCT scanning

Y仪器型号及参数	CT METROTOM 1500 225 kV
射线管输出功率/W	300‒450
射线管输出电压/kV	189‒200
射线管输出电流/μA	1.80×10³‒2.50×10³
仪器最小分辨率/μm	7
满足上述条件的湿度	18‒22 ℃, 2.0 K∙d⁻¹, 1.0 K∙m⁻¹, 40%‒70% (无凝结)

图2 XCT影像的二值化图像样例

Figure 2 Binary image of XCT

图3 XCT灰度图像样例及其灰度分布图

Figure 3 Gray scale images and gray value distribution of XCT

图4 GAN模型训练流程

Figure 4 Execution procedure of GAN

表2 GAN模型训练参数

Table 2 Training parameters of GAN

参数	石英砂	土壤
原始图像大小	500³	650³
训练图像大小	64³	64³
批处理数据量	4	4
学习率	10⁻⁵	10⁻⁵
迭代次数	1000	1000
GPU数量	4	4
优化器	Adam	Adam
第一动量衰减因子	0.999	0.999
Z向量大小	512	512
模型稳定性方法	White Noise (σ=0.1)	White Noise (σ=0.1)

表3 CFD数值模拟参数

Table 3 Parameters of CFD simulation

参数	石英砂
粘度η/(Pa·s)	0.010
流体密度ρ/(kg·m⁻³)	1.00
重力加速度g/(m·s⁻²)	9.80

表4 CFD数值模拟条件

Table 4 Conditions of CFD simulation

模拟条件	压力场p	速度场u
初始条件	均质场，0
入口条件	出入口, 均值10⁻⁵	零梯度
出口条件	固定值, 均值0	零梯度
上边界条件	循环	循环, 均值0

图5 XCT合成数据与GAN模型训练数据与合成数据对比图

Figure 5 Original image scanned by XCT and synthetic image generated by GAN

图6 损失函数曲线

Figure 6 The loss function curve

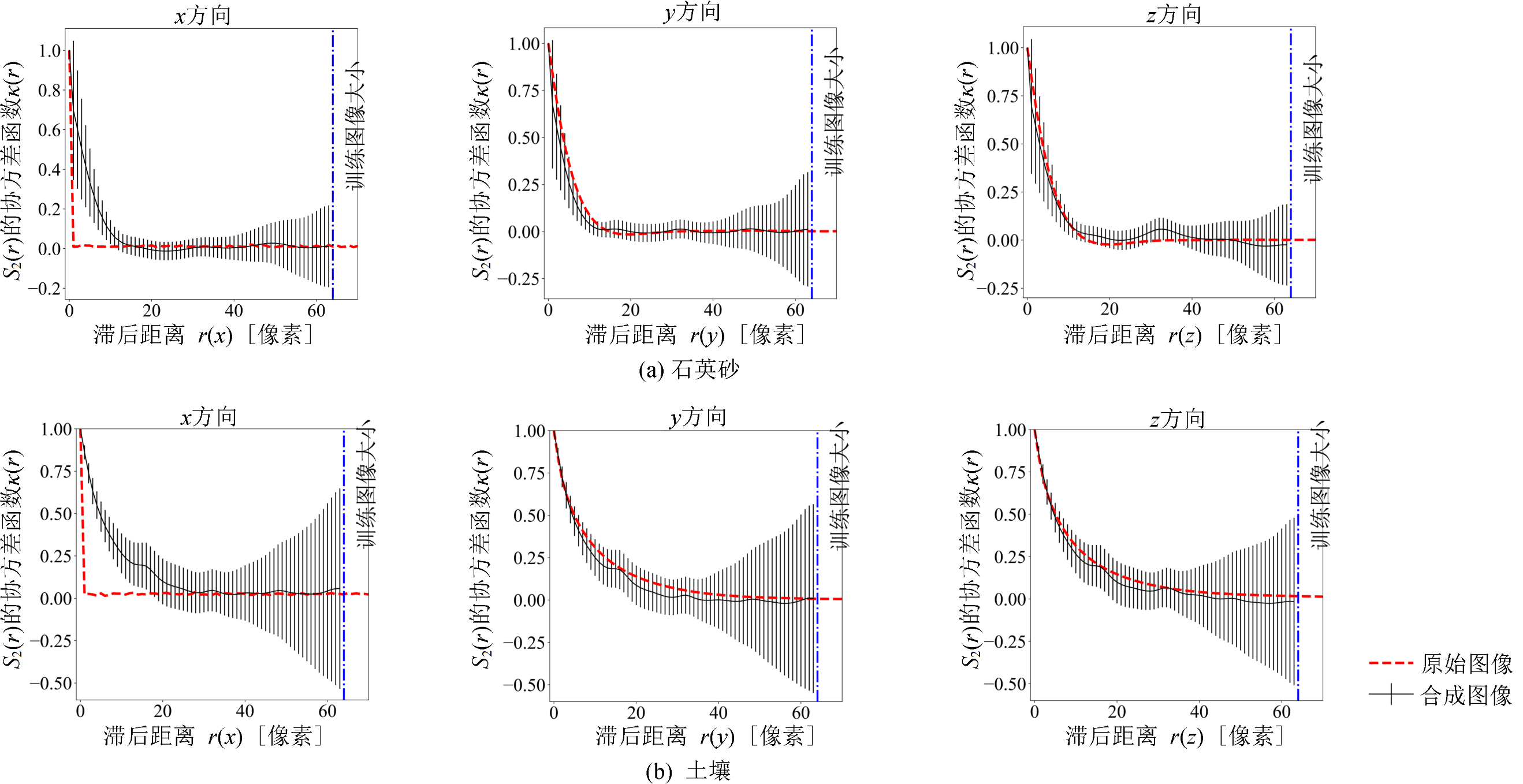
图7 x、y、z三方向标准化后被向量r分割的两点属于孔隙的概率

Figure 7 Normalized probability from x, y, and z direction of two points connected by vector r that belongs to pore space

图8 被向量r分割的两点属于孔隙的概率（三方向平均）

Figure 8 Normalized probability of two points connected by vector r that belongs to pore space

图9 训练图像与合成图像的Minkowski参数对比图

Figure 9 Minkowski functionals of training images and synthetic images

表5 Minkowski参数评价结果

Table 5 Results of Minkowski functional evaluation

评价指标	石英砂		土壤
评价指标	训练数据	合成数据	训练数据	合成数据
平均孔隙弦长 [像素](变量)	8.62	13.6	10.9	18.6
平均粒径弦长 [像素] (变量)	11.5	17.7	10.2	17.6
孔隙度 (变量)	0.428	0.433	0.517	0.534
表面面积 (变量)	1.60×10⁻⁸	1.65×10⁻⁸	1.62×10⁻⁸	1.65×10⁻⁸
平均曲率 (变量)	2.89×10⁻¹¹	1.59×10⁻¹¹	1.99×10⁻¹⁰	1.25×10⁻¹⁰
欧拉数 (变量)	−2.22×10⁻¹¹	−2.74×10⁻¹¹	−2.02×10⁻¹¹	−2.74×10⁻¹¹

图10 训练图像与合成图像的Minkowski参数随孔隙体积的变化

Figure 10 Variation of Minkowski functionals of training images and synthetic images with the change of porosity

图11 石英砂和土壤渗透率随孔隙度变化图

Figure 11 Permeability of sand and soil with porosity variation

参考文献 33

[1]	BLUNT M J, 2017. Multiphase flow in permeable media: A pore-scale perspective[M]. Cambridge: Cambridge University Press.
[2]	BULTREYS T, DE BOEVER W, CNUDDE V, 2016. Imaging and image-based fluid transport modeling at the pore scale in geological materials: A practical introduction to the current state-of-the-art[J]. Earth-Science Reviews, 155: 93-128. DOI URL
[3]	BULTREYS T, BOONE M A, BOONE M N, et al., 2015. Real-time visualization of Haines jumps in sandstone with laboratory-based microcomputed tomography[J]. Water Resources Research, 51(10): 8668-8676. DOI URL
[4]	CHUNG S Y, KIM J S, DIETMAR S, 2019. Overview of the use of micro-computed tomography (micro-CT) to investigate the relation between the material characteristics and properties of cement-based materials[J]. Construction and Building Materials, 229(1168): 43-55.
[5]	FULLWOOD D T, NIEZGODA S R, KALIDINDI S R, 2008. Microstructure reconstructions from 2-point statistics using phase-recovery algorithms[J]. Acta Materialia, 56(5): 942-948. DOI URL
[6]	GARCIA-GARCIA A, ORTS-ESCOLANO S, OPREA S, 2018. A survey on deep learning techniques for image and video semantic segmentation[J]. Applied Soft Computing, 70: 41-65. DOI URL
[7]	GOODFELLOW I, POUGET-ABADIE J, MIRZA M, et al., 2020. Generative adversarial networks[J]. Association for Computing Machinery, 63(11): 139-144.
[8]	GRACZYK K M, MATYKA M, 2020. Predicting porosity, permeability, and tortuosity of porous media from images by deep learning[J]. Scientific Report, 10(1): 1-11.
[9]	GUIBERT R, NAZAROVA M, HORGUE P, 2015. Computational permeability determination from pore-scale imaging: Sample size, mesh and method sensitivities[J]. Transport in Porous Media, 107: 641-656. DOI URL
[10]	HORGUE P, SOULAINE C, FRANC J, 2015. An open-source toolbox for multiphase flow in porous media[J]. Computer Physics Communications, 187: 217-226. DOI URL
[11]	HÜTTER M, 2003. Heterogeneity of colloidal particle networks analyzed by means of Minkowski functionals[J]. Physical Review E, 68(3): 031404. DOI URL
[12]	JI X M, QIAN J, RAHMAN S M J, et al., 2018. XCT (SLC7A11)-mediated metabolic reprogramming promotes non-small cell lung cancer progression[J]. Oncogene, 37(36): 5007-5019. DOI PMID
[13]	KAMRAVA S, TAHMASEBI P, SAHIMI M, 2020. Linking morphology of porous media to their macroscopic permeability by deep learning[J]. Transport in Porous Media, 131: 427-448. DOI
[14]	KATO M, KANEKO K, TAKAHASHI M, 2015. Segmentation of multi-phase X-ray computed tomography images[J]. Environmental Geotechnics, 2(2): 104-117. DOI URL
[15]	KLAIN D A, ROTA G C, 1997. Introduction to geometric probability[M]. Cambridge: Lezioni Lincee.
[16]	MAAS A L, HANNUN A Y, NG A Y, 2013. Rectifier nonlinearities improve neural network acoustic models[J]. Journal of Machine Learning Research, 30(28): 1-6.
[17]	MATHERON G, 1971. Elements pour une theorie des milieux poreux[M]. Paris: Masson.
[18]	MOSSER L, DUBRULE O, BLUNT M J, 2017. Reconstruction of three-dimensional porous media using generative adversarial neural networks[J]. Physical Review E, 96: 043309. DOI URL
[19]	NIEZGODA S R, FULLWOOD D T, KALIDINDI S R, 2008. Delineation of the space of 2-point correlations in a composite material system[J]. Acta Materialia, 56(18): 5285-5292. DOI URL
[20]	REIJONEN H M, KUVA J, HEIKKILA P, 2020. Benefits of applying X-ray computed tomography in bentonite based material research focused on geological disposal of radioactive waste[J]. Environmental Science and Pollution Research, 27(38): 407-421.
[21]	RIESCO R, BOYER L, BLOSSE S, 2019. Water-in-PDMS emulsion templating of highly interconnected porous architectures for 3D cell culture[J]. American Chemical Society, 11(286): 31-40. DOI URL
[22]	SAHIMI M, 2003. Heterogeneous materials I: Linear transport and optical properties[M]. New York: 175 Fifth Avenue.
[23]	SCHLÜTER S, SHEPPARD A, BROWN K, et al., 2014. Image processing of multiphase images obtained via X-ray microtomography: A review[J]. Water Resources Research, 50(36): 15-39.
[24]	SCHOLZ C, WIRNER F, KLATT M A, 2015. Direct relations between morphology and transport in Boolean models[J]. Physical Review E, 92: 043023. DOI URL
[25]	SERGEY I, CHRISTIAN S, 2015. Batch Normalization: Accelerating deep network training by reducing internal covariate shift[J]. Proceedings of Machine Learning Research, 37: 448-456.
[26]	SUDAKOV O, BURNAEV E, KOROTEEV D, 2019. Driving digital rock towards machine learning: Predicting permeability with gradient boosting and deep neural networks[J]. Computers & Geosciences, 127: 91-98. DOI URL
[27]	TOWNSEND A, PAGANI L, SCOTT P, et al., 2017. Areal surface texture data extraction from X-ray computed tomography reconstructions of metal additively manufactured parts[J]. Precision Engineering, 48(4): 72.
[28]	VARFOLOMEEV I, YAKIMCHUK I, SAFONOV I, 2019. An application of deep neural networks for segmentation of microtomographic images of rock samples[J]. Computers, 8(4): 1-21. DOI URL
[29]	WANG F, CHENG Y, LU S, 2014. Influence of coalification on the pore characteristics of middle-high rank coal[J]. Energy & Fuels, 28(57): 29-36.
[30]	WANG H, YIN Y, HUI X Y, et al., 2020. Prediction of effective diffusivity of porous media using deep learning method based on sample structure information self-amplification[J]. Energy and AI, 2: 100035. DOI URL
[31]	WU H Y, FANG W Z, KANG Q J, 2019. Predicting effective diffusivity of porous media from images by deep learning[J]. Scientific Report, 9: 20387.
[32]	ZHANG F, TENG Q Z, CHEN H G, 2021. Slice-to-voxel stochastic reconstructions on porous media with hybrid deep generative model[J]. Computational Materials Science, 186: 110018. DOI URL
[33]	ZHANG Y T, JIANG F, TSUJI T, 2022. Influence of pore space heterogeneity on mineral dissolution and permeability evolution investigated using lattice boltzmann method[J]. Chemical Engineering Science, 247: 117048. DOI URL

应用XCT断层扫描技术和GAN深度学习模型的多孔介质微观结构定量研究

Reconstruction of Porous Media Microstructure Via X-ray Computed Tomography and Generative Adversarial Networks

RichHTML

PDF

可视化

摘要/Abstract

引用本文

使用本文

图/表 16

参考文献 33

相关文章 15

编辑推荐

Metrics

本文评价

[1]	王郑钧, 王邵军, 肖博, 解玲玲, 郭志鹏, 张昆凤, 张路路, 樊宇翔, 郭晓飞, 罗双, 夏佳慧, 李瑞, 杨胜秋, 兰梦杰. 西双版纳热带森林土壤有机碳积累-分配动态对蚂蚁筑巢活动的响应[J]. 生态环境学报, 2024, 33(1): 35-44.
[2]	袁佳宝, 宋艳宇, 刘桢迪, 朱梦圆, 程小峰, 马秀艳, 陈宁, 李晓宇. 松嫩平原芦苇湿地土壤酶活性剖面分布特征及其微生物养分限制指示作用[J]. 生态环境学报, 2023, 32(12): 2141-2153.
[3]	李璇, 钱秀雯, 黄娟, 王鸣宇, 肖君. 纳米氧化镍暴露下人工湿地运行性能及微生物群落的响应[J]. 生态环境学报, 2023, 32(10): 1833-1841.
[4]	肖成志, 计扬, 李建忠, 张志, 巴仁基, 曹亚廷. 岷江上游生态脆弱性时空分异及驱动因子交互效应分析——以杂谷脑河流域为例[J]. 生态环境学报, 2023, 32(10): 1760-1770.
[5]	刘晨, 白雪冬, 赵海超, 黄智鸿, 刘松涛, 卢海博, 刘子刚, 刘雪玲. 寒旱区春玉米秸秆还田方式对土壤DOM光谱特征的影响机制[J]. 生态环境学报, 2023, 32(8): 1419-1432.
[6]	陈懂懂, 霍莉莉, 赵亮, 陈昕, 舒敏, 贺福全, 张煜坤, 张莉, 李奇. 青海高寒草地水热因子对土壤微生物生物量碳、氮空间变异的贡献——基于增强回归树模型[J]. 生态环境学报, 2023, 32(7): 1207-1217.
[7]	李海鹏, 黄月华, 孙晓东, 曹启民, 符芳兴, 孙楚涵. 海南农田不同质地砖红壤及其细菌群落与番茄青枯病发生的关联分析[J]. 生态环境学报, 2023, 32(6): 1062-1069.
[8]	周玉祥, 赵玉, 聂仁东, 丁丁, 郭立华, 周佳峥. 下辽河平原土地沙漠化程度及预测研究[J]. 生态环境学报, 2023, 32(6): 1133-1139.
[9]	王琳, 卫伟. 黄土高原典型县域生态系统服务变化特征及驱动因素[J]. 生态环境学报, 2023, 32(6): 1140-1148.
[10]	刘霞, 郭澍, 王琳. 区域一体化地区的土地利用与生态服务价值研究——以双莱先行区为例[J]. 生态环境学报, 2023, 32(6): 1163-1172.
[11]	董智今, 张呈春, 展秀丽, 张维福. 宁夏河东沙地生物土壤结皮及其下伏土壤养分的空间分布特征[J]. 生态环境学报, 2023, 32(5): 910-919.
[12]	王超, 杨倩楠, 张池, 刘同旭, 张晓龙, 陈静, 刘科学. 丹霞山不同土地利用方式土壤磷组分特征及其有效性[J]. 生态环境学报, 2023, 32(5): 889-897.
[13]	李传福, 朱桃川, 明玉飞, 杨宇轩, 高舒, 董智, 李永强, 焦树英. 有机肥与脱硫石膏对黄河三角洲盐碱地土壤团聚体及其有机碳组分的影响[J]. 生态环境学报, 2023, 32(5): 878-888.
[14]	周沁苑, 董全民, 王芳草, 刘玉祯, 冯斌, 杨晓霞, 俞旸, 张春平, 曹铨, 刘文亭. 放牧方式对高寒草地瑞香狼毒根际土壤团聚体及有机碳特征的影响[J]. 生态环境学报, 2023, 32(4): 660-667.
[15]	潘昱伶, 璩向宁, 李琴, 王磊, 王筱平, 谭鹏, 崔庚, 安雨, 佟守正. 黄河宁夏段典型滩涂湿地土壤理化因子空间分布特征及其对微地形的响应[J]. 生态环境学报, 2023, 32(4): 668-677.